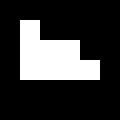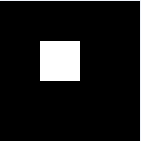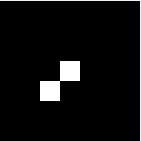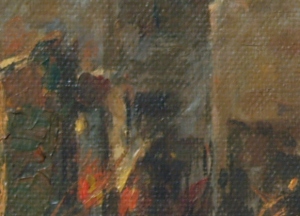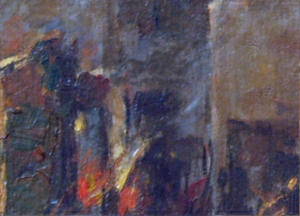Activity 9 – Basic Video Processing

And at last we arrive at this moment. This is the time to blog about the last activity of Applied Physics 186. This is the last activity of the sem and hopefully my last required blog for my bachelor’s degree. 🙂 This subject gave me some new skills that I know I would be able to effectively use for other purposes at some time. And one of them is this activity, basic video processing.

A video could be viewed as a set of images that are in sequence with one another shown in very rapid succession. Because of this concept, we would be able to study in detail the motion of an object or how something spreads. There are many practical applications of video processing such as the study of the growth of a bacteria, the motion of an athlete in sports and the motion of a falling object.

Each digital video has a frame rate or fps which indicates the number of frames or images that the camera we used can capture in a second. This means that for every pair of succeeding image has a time interval of the inverse of the frame rate. By knowing these concepts, we can study the time dependent parameters using images from videos such as a motion of an object.

For this activity, we investigate the free fall of an umbrella. We go back to the concept of kinematics to observe the motion of the object. Without air resistance, the object has an acceleration equal to g, or 9.8 m/ $s^2$ . But in real systems, we know that there is a drag force that stops the object from falling with an infinite velocity. At some point in time, this drag force would soon be equal to the force due to gravity. The velocity of the object at this point of time is the terminal velocity.

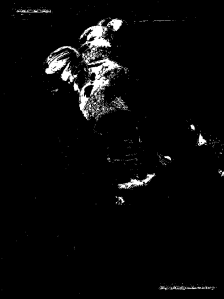
In this activity, I paired up with Martin Bartolome to investigate the free fall of an umbrella. First and foremost, I would like to thank our hero, Mario Onglao for lending us his blue umbrella without hesitation. Without your kindness, this activity would not have been possible for us. And as proof that we performed this experiment, first let us take a selfie!

selfie

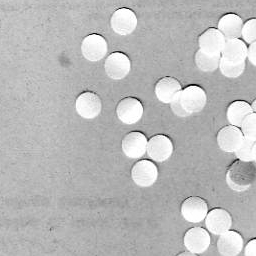
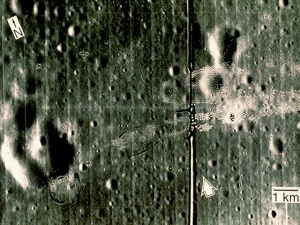
We took advantage of the height of the very beautiful NIP building to perform the experiment. We drop the umbrella from the fourth floor of NIP and Barts received the umbrella at the ground floor. With the help of Dr. Soriano (maam thank you!), we were able to capture the experiment using her Olympus DSLR camera. We present a GIF version of the video.

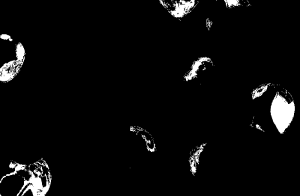
Figure 1: GIF version of a portion of the original video clip which shows the free falling of a blue umbrella

The GIF image is from a 4 second clip from the original video captured. It features the exact time I released the umbrella until it reaches the hands of Barts. It is obviously slower than the original pace of the video for its purpose if for us to at least observe the motion of the umbrella as it reaches its terminal velocity. And by observation we could observe this phenomenon and we wish to prove it using the video processing technique. But first I want to note that the camera used has a frame rate of 59 fps. Since this would require me to have a large number of images to be processed, I chose to reduce the frame rate to 15 fps for my analysis. I think that the chosen frame rate would be enough for this purpose.

To perform video processing, we must first obtain the images by any software that could help. According to the manual given to us, some suggested softwares are STOIK Video Converter for video format conversion and VirtualDub for extracting images from the video. But there was a problem with the format of the video we have. It is in MTS format and the STOIK Video Converter cannot convert this so we cannot use these softwares. Good thing I ask Gio Jubilo for some help and he pointed out about some video to jpg converter. Upon searching, I found the free DVDVideoSoft software. It contains a Video to JPG converter mode. This is the software I used to extract the images from the video. I used the parameter 15 fps to extract the images from the video.

We note again that the time interval between succeeding images I obtained is the inverse of the frame rate. So the time interval is equal to 1/15 or 0.0667 seconds which should be enough for a 4 second clip for video processing. Of course with a choice of a larger frame rate, we could be assured of a higher accuracy of analysis but also a higher need of processing power. The choice of frame rate for image extraction should depend on the purpose of the user.

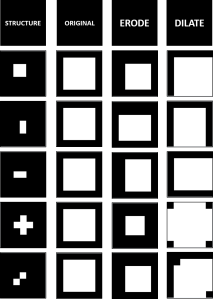
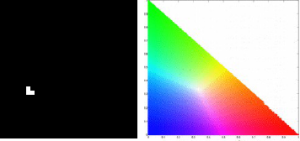
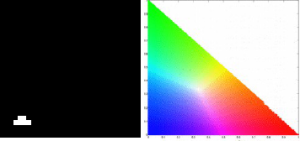
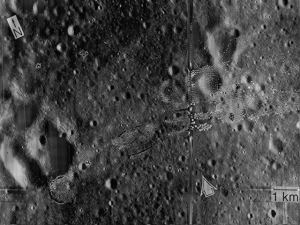
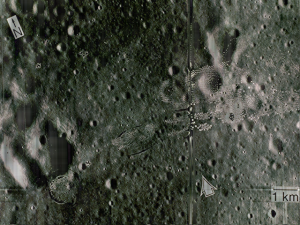
From these images we would be able to determine the velocity of the umbrella during its free fall. For the sequence of image, we could locate the centroid of the umbrella and know its distance from the initial position. We would be able to do this by image segmentation as we previously learned from Activity 7. Since we have the skills for this purpose, we can immediately go through the process. There are two kinds of image segmentation and from the activity, we observed that the non-parametric segmentation is the more flexible and efficient method. Even though it requires a lot of processing time, the results are unmatched. For this activity, I applied the non-parametric segmentation to the 61 images obtained and used the patch shown below as our region of interest (ROI).

patch

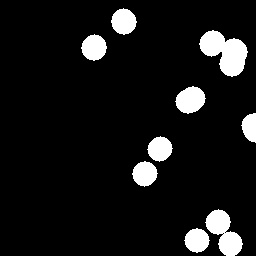
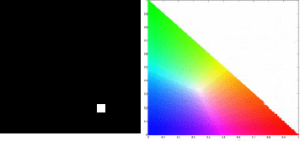
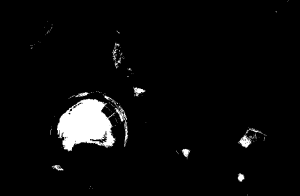
The patch is a part of the umbrella. Good thing that the color of the umbrella stands out from the background therefore we were able to segment the umbrella from the surrounding. After segmenting, we observe that there are still stray intensities away from the location of the umbrella. This problem would affect our search for the location of the centroid of the umbrella for each time step. Therefore learning about morphological operations in Activity 8, we know that we could remove these stray values and retain the shape of the umbrella. We use the Open operator and a circular structuring element of radius 7 pixels to clean the stray intensities and retain the shape of the umbrella. The operator first erodes the stray values then dilates or maintain the shape of the umbrella. After doing all these image segmentation and morphological operations, the finish product is shown in GIF format below.

Figure 2: GIF version of the segmented images from the video. The morphological operator, Open, was also used.

The patch I used to segment the umbrella is from an image where it is still on top of the 4th floor. From the original clip of the video, we can observe that at the start of the free fall, the umbrella is illuminated by the sun. The patch is from this portion of the video which can also explain the diminishing shape of the umbrella. The morphological operator, Open, might also be a cause for the diminishing shape. There was also a part of the motion where the umbrella partly tilted in the z-axis therefore the shape diminished at that point. The centroid was calculated by taking the mean value of the coordinates of the white pixels of the segmented shape of the umbrella.

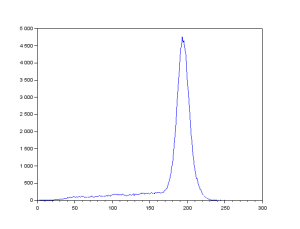
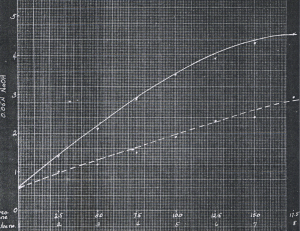
The distance is calculated for each centroid of every image from the initial position. Knowing the time step for each pair of succeeding image, we plot the distance vs time plot. But before I forget, first things first. We took the distance of the centroid in pixel units. We convert this into a real physical unit. We were able to measure the distance between the floors of the second and third floors of the building which is 84 inches. By using this measurement, we learned that the conversion factor is 0.168 inches / pixel. The plot is shown below.

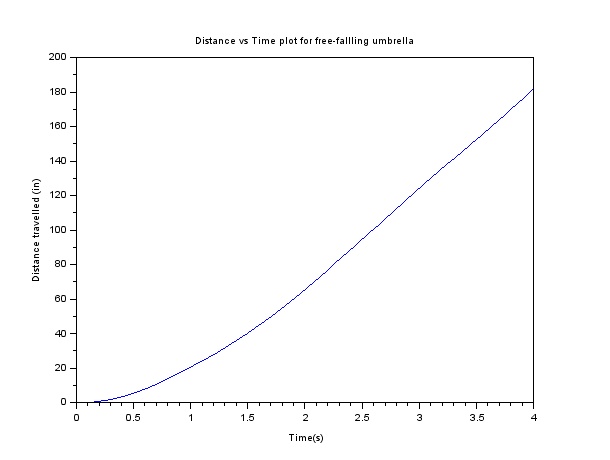
Figure 3: Distance vs Time plot for the free fall motion

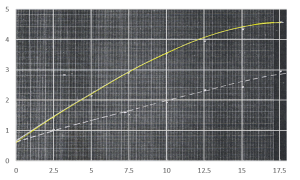
And voila! The object seems to pick up its velocity in the first moments then maintain a steady velocity in the later parts of its free fall. This velocity is our terminal velocity where the drag force is already equal to the force of gravity on the object. We simply take the slope of the linear plot to obtain this value. I tried to plot the linear regression using Scilab but then I do not know how to place the equation of the line in the plot’s legend. I used Excel instead to plot the linear regression of the plot. Fortunately, the equation of the line I obtained in Scilab is the same with the Excel plot I obtained. This is the linear regression of the plot of the distance vs time of the free fall of the umbrella.

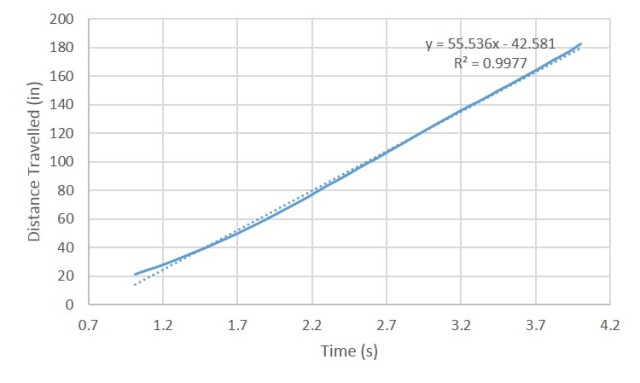
Figure 4: Linear Regression of the linear plot

You can observe that I cut the plot and started at about 1 second since the umbrella was still picking up its velocity on earlier times as shown by the curve of the motion plot. We obtain a 55.536 slope which means that the terminal velocity is 55.536 inches/second or about 1.41 m/s which is realistic. We can also observe this in the original video clip we have.

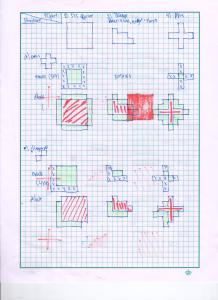
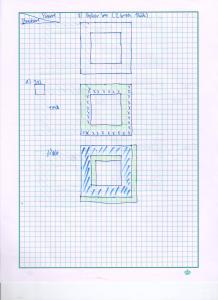
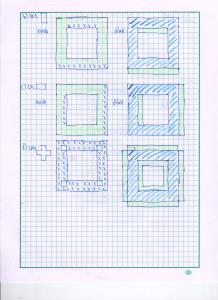
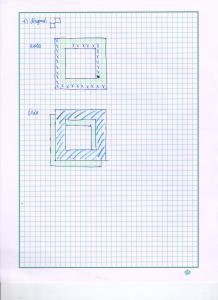
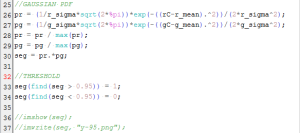
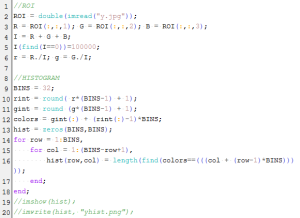
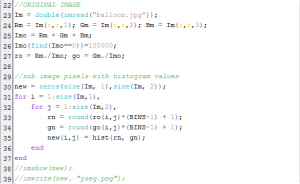
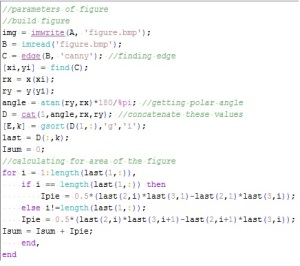
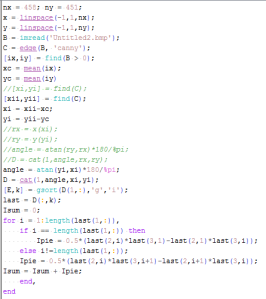
By this experiment, we prove that we can use video processing to investigate some physics concepts and obtain good data. I am very thankful for this activity because I was able to use some other skills I learned from previous activities which was really fun. I hope that I can still use these skills in the near future. And ooops, before I end this activity, these are snapshots of my Scilab code I used for segmenting, application of the morphological operator and plotting for this activity.

For this activity, I would like to give myself a 10/10 since I was able to present the concepts and results properly. I was also able to perform the skills and technique well. I want to also give myself an extra 2 points since I believe that I presented a great quality of work. By this self-evaluation, I end my Applied Physics 186 blog series. I hope I can still post some time on this blog and share some more things I would learn in the future. Thank you Maam Jing for these new skills and fun you showed us through these challenging activities. We will cherish these activities which I know are out of the box activities. 😀

And since this is the last activity blog, please bear with me with these emotions.

And because I am really happy, please give me some.

himym

Activity 8 – Morphological Operations

Morphological operations are used in image processing to process or extract information from a binary image. Usually these binary images are aggregates of 1’s forming a particular shape. These morphological operations affects the shape of the image in any way. The shape might be expanded, thinned or closing of internal holes and disconnected blobs can be joined. For numerical calculation of this operation, we represent our black background with 0’s and our shape with series of 1’s.

The concept behind the morphological operations is the Set Theory. The concepts of being an element of a set (∉), subset (⊂), union (∪), intersection (∩), empty set (Ø), complement (C), difference (A-B), reflection and translation comprises the basic what to know about morphological operations. Combining all these concepts, we simplify and discuss just two of the morphological operations: Erosion and Dilation.

Dilation is defined as,

A $\oplus$ B = { z | $( \hat{B} )_z$ ∩ A ≠∅ }

B is defined as the structuring element. All z’s which are translations of a reflected B when intersected with A is not an empty set. Dilation aims to expand or elongate A in the shape of B. An example is given below.

Erosion is defined as,

A ⊖ B = {z| $(B)_z$ ⊆ A }

The erosion of A by the structuring element B is the set of all points z such that B translated by z is contained in A. Erosion aims to reduce the image A by the shape B. An example is shown below.

Erosion and dilation are duals of each other thus the relationship follows,

(A ⊖ $B)^{c}$ = $A^c \oplus B$

Exercises

To observe erosion and dilation, we did an exercise to predict and observe the erosion and dilation of 4 binary shapes to each of the 5 available structuring elements. The 4 binary shapes are the 5×5 square, a triangle with base of 4 boxes and height of 3 boxes, a hollow 10×10 square which is 2 boxes thick and a plus sign which is 1 box thick and has 5 boxes along each line. These shapes are shown below.

The structuring elements used for the exercise are a 2×2 ones, 2×1 ones, 1×2 ones, a cross which is 3 pixels long and 1 pixel thick and a diagonal line which is 2 boxes long. These structures are shown below.

To get a better grip on the concept of the morphological operations, I draw these shapes and predicted their results after erosion and dilation on a graphing paper. The results I obtained is shown in 5 images below.

To check my predictions, I used the Image Processing Design (IPD) module of Scilab. I performed the morphological operations to each binary shape for each structuring element. The results are as follows for the 5×5 square, triangle, hollow box and a plus sign respectively.

Res2

Res3

Res4

Comparing my manual prediction to the results in Scilab, I believe I had a better understanding of the concepts of erosion and dilation. I obtained the same results for each figure. As we can observe, in erosion, a pixel is eroded if the structuring element is not fitted in the binary image. That is, if the structuring element is placed in the pixel and not all pixels of the structuring element is an element of the binary shape, the certain pixel is eroded or zeroes out. In dilation, if the structuring element is not fitted in the binary image, the binary shape is expanded following the shape of the structuring element.

Application

After observing and discussing erosion and dilation, we observe three other morphological operations: Open, Close and TopHat. These morphological operators are a product of the erosion and dilation of binary images. We further discuss these operations.

Open operation involves preserving the foreground regions that have a similar shape to the structuring element while eliminating all the other regions of foreground pixels. In simple terms, the open operation is defined as an erosion followed by a dilation using the same structure element. Simply, open = dilate(erode(shape, element), element).

Close operation is a dual of opening. It involves preserving the background regions that have a similar shape to the structuring element while eliminating all other regions of background pixels. In simple terms, the close operation is defined as a dilation followed by an erosion using the same structure element. Simply, close = erode(dilate(shape, element), element).

TopHat transform is also called the peak transform. A binary image applied by an open operator by a structuring element is subtracted from the original image. The brightest spots on the original image are highlighted using this transformation. In simple terms, tophat = shape – open(shape, element).

To observe these operations, we used them in a simple application of these operations. A well known application of the morphological operations is the identification of cancer cells from normal cells. We simulate this application using the figure below. It shows “cancer cells” (bigger cells) joint along the “normal cells” represented by punched paper bits.

To perform the identification of cancer cells, we first examine the normal cells. We aim to know the area of the normal cells to isolate them with the cancer cells. We use the image below to calculate the approximate area of the normal cells.

To have a better approximation of the area, we divide the original image into 10 subimages of size 256×256. We would be able to get more data points and have a better calculation of the area of a normal cell. We apply the open, close and tophat operators to a subimage to observe the effects of these operators. The structural element used is a circle of radius 12. The subimage used and its grayscale version are shown below.

Open operator:

Close operator:

TopHat operator:

We can observe in the grayscale version of the subimage used that it still has unwanted white spots that are not part of the “normal cells”. The normal cells are also not “whole” in the sense that there are missing parts of the circle. Using the morphological operators, we observe some things. The open operator clearly removes these white spots and made the “normal cells” whole. The close operator connects the cells and distorts the image by doing so. The tophat operator as defined subtracts the image produced by the open operator to the original image. By these results, we opt to use the open operator to identify the cancer cells.

Now that we have the operator to use for our cause, we first approximate the area for the normal cells. We apply the open operator for the 10 subimages using a circular structuring element. We search for blobs using the SearchBlobs command of the module of Scilab. It automatically label each blob and calculate each area in terms of number of pixels. After obtaining the area of each blob, we plot the histogram of the number of blobs with the blob area. The histogram is shown below.

Most of the normal cells are in sizes between 300-600 square pixels. Areas below are small enough to be considered normal cells. Clump of cells are the ones with areas greater than 600 square pixels. We get the mean area using these values. To have a flexibility of the approximate area, we also calculate the standard deviation for the area of the cells. Now we have an approximate area for our normal cells.

We move on with the image with the cancer cells and normal cells. We apply the open operator with the grayscale version of the image by a circular structuring element with radius 13. We label the blobs with the same command and created a size histogram shown below.

After applying the open operator, we can observe in the histogram that the normal cells are the ones with the area less than 600 square pixels. A group of peaks greater than this value can be considered as the cancer cells and some clump of normal cells. We remove these normal cells by taking into consideration the blobs with areas within the range of (mean area – standard deviation) to (mean area + standard deviation). We also remove the clumps of normal cells. The resulting image is shown below.

We were able to isolate the cancer cells using the open operator and the size histogram. In this way, we see the application of the morphological operations in identifying cancer cells from normal cells. From the original image, we could already identify the cancer cells. We successfully isolated the cancer cells.

Review and Self-Evaluation

I was able to learn the concepts of morphological operators. Applying these operators, we were able to observe a well known application of the morphological operators. The “cancer cells” in the image were identified and isolated to the “normal cells”. Because of these factors I would give myself 10 points for being able to follow instructions and present my results in an organized manner. I was not able to have another activity beyond the given instructions so I would not deserve some bonus points.

Overall, I would like to thank Jaime Olivares for providing some graphing paper during the activity, Ron Aves, Ralph Aguinaldo and Gio Jubilo for helping me sort out some issues I had with the activity. Thank you to Dr. Soriano for her continuous patience on us.

References:

A8 – Morphological Operations, Dr. Maricor Soriano, Applied Physics 186 Manual
http://homepages.inf.ed.ac.uk/rbf/HIPR2/open.htm
http://homepages.inf.ed.ac.uk/rbf/HIPR2/close.htm
http://www.inf.u-szeged.hu/ssip/1996/morpho/morphology.html

Activity 7 – Image Segmentation

Image segmentation. We would not manually cut desired parts of the image since that would require too much work. Instead, we would use the concept of image segmentation to separate different desired parts of the image such as colors. The process requires the binarization of the image through a threshold that would be set for the image.

For a certain region of interest, we would separate this region and the parts of the image which contains the same properties and isolate them. The binarization process converts the colored image into an image composed of black and white. Upon isolation, it is upon us on what to represent the isolated parts of the image. To give us a good look, we observe an example.

Grayscale Image Segmentation

We considered a check in grayscale. Suppose we desire to isolate the hand writings and computer generated scripts in the check, we refer to the Scilab code given from the manual.

The code starts by investigating on the histogram of the grayscale image. The histogram would tell us the details about the pixel values of the grayscale image. The histogram can be seen below.The peak location in the histogram corresponds to the background of the check. We can infer that they cover a lot more space than the text in the check. By choosing a threshold of 125 as shown in Line 6 of the code, we could separate the text completely from the background. The result can be seen as follows.

The result clearly shows that we have segmented the text from the check. We can also try different thresholds to observe if we could improve more on our segmentation. This is the case for grayscale images but as can be seen in the image below, it does not always work this way.

Because of this tragedy, we consider color segmentation for our images. Color is one good parameter to consider to separate regions of interest from the image. It has long been used to segment images of skin regions in faces, and
hand recognition, land cover in remote sensing, and cells in microscopy [1].

For this reason, we should consider a representation of the color space. We also need to consider the shading variations in different images where shadows darkens some colors but knowing the image, we could observe the same color for two regions. To disregard this minor problem, we would consider a color space that can separate brightness and chromaticity information [1]. This color space is the normalized chromaticity coordinates or NCC.

We first normalize the RGB coordinates by this way,

$r = \frac{R}{I}$ , $g = \frac{G}{I}$ , $b = \frac{B}{I}$

where $I = R + G + B$ . We can take note that $r + g + b = 1$ . We further simplify the coordinate system by setting the dependence of the blue channel with red and green channels, $b = 1 - r - g$ . We then can represent chromaticity with just two coordinates, r and g. The variable I would contain brightness information. The NCC can be seen as such.

We clearly can see the dependence of the blue coordinate with the other two. When both r and g are zero, b =1 which is still consistent with the unity of all coordinate channels. Two methods of image segmentation are presented for this activity. For both activity we would try to segment the following images.

Civil War comic strip obtained from http://www.vox.com/2014/10/14/6973309/robert-downey-jr-captain-america-3-movie

Obtained from http://polygonblog.com/3d-birthday-balloons-in-3ds-max/

The patches considered for each images for the whole activity is given below.

The top set of 2 patches were used for the Civil War (CW) image while the bottom set of 4 patches were used for the Balloon (B) image.

Parametric Segmentation

In parametric segmentation, we consider a color distribution of interest to determine the probability of a pixel belonging to the region of interest. We first crop a region of interest and observe the histogram of the region of interest. Since we are considering the NCC, we would find the probability that a pixel belongs to the region of interest (ROI) by finding the probability that the pixel belonging to the color of the ROI. We consider both probabilities for the red and green coordinates of our NCC. The probability that the pixel belongs to the ROI is given by the equation,

$p(c) = \frac{1}{\sigma_{c}\sqrt{2\pi}}exp(-\frac{(c - \mu_{c})^2}{2\sigma_{c}^{2}})$

where c is the color red or green. $\mu$ and $\sigma$ are the mean and standard deviation from the pixel samples. To tag a pixel as belonging to the ROI, we would consider the joint probability, $p(r)p(g)$ .

The simple code used for the parametric segmentation of the two images is shown below.

We first converted the RGB coordinates of the ROI into the NCC in Lines 1-8. The mean and standard deviations of these coordinates were calculated in Lines 10-14. The RGB coordinates are also converted into the NCC in Lines 16-23. The joint probability distribution is obtained in Lines 25-30. We placed different thresholds to observe image segmentation. Upon applying the code, we look into results of parametric segmentation in 2 images considered.

The CW image was segmented using the blue patch as ROI. Segmentation with different thresholds ranging from 0.75 – 0.95 with increments of 5 were produced. As we can observe the higher the threshold, the better segmentation we can obtain. The last image proves the power of segmentation, clearly isolating the blue uniform and some parts of the shield of Captain America. It was an awesome piece of art for me since through simple calculations of probability distributions, we can segment the some regions of an image. For the red patch, we obtain the following results,

The CW image was segmented using the red patch as ROI. Segmentation with different thresholds ranging from 0.75 – 0.95 with increments of 5 were produced. The same kind of results were obtained, noting that the last image clearly isolates the red steel of Iron Man.

For a fun kind of segmentation, I had fun in the next image considered. Some results are as follows.

From left to right for all sets of results, the thresholds considered are 0.90 and 0.95 respectively. The first two sets used a patch of blue. There was a big difference in the two results. Referring to the original image, we can clearly choose that the right result is the one with the threshold of 0.95. The other result considered the purple balloons as part of the region of interest which we can forgive since blue and violet are colors which are close to each other.

The next two sets used a green patch as ROI. Both results are favorable but the image with a threshold of 0.90 considered the blue green balloons to be part of the ROI. But thresholds were used to eliminate some of these mistakes.

The 3rd set used a red patch as ROI. With threshold of 0.9, the returned image considered some orange balloons as part of the ROI. But then with the threshold raised to 0.95, only red balloons were considered. This set was the best set for me since I was amazed that the algorithm used denied the entry of the window-like shadow and some reflection in the right most red balloon.

The 4th and last set used a patch of yellow for ROI. For both results, orange balloons were considered. Somehow even with a high threshold, some of these errors occurs. I believe that changing and being careful of choosing the ROI could avoid this kind of mistakes.

Overall, the method of parametric segmentation proves to be a good and accurate choice for image segmentation. Though we could note that for larger sizes of image, a larger processing time would be expected. These are some important factors we need to consider for choosing our method of image segmentation in the future.

Non-parametric Segmentation

In parametric segmentation, we basically fit an analytic function to the histogram to create a function in checking if the pixel of an image belongs to the ROI. But the method’s accuracy depends solely on the goodness of the fit of the probability distribution function considered.

In the non-parametric segmentation, we use the histogram itself to admit the pixel as member of the ROI. A technique called histogram backprojection is necessary to perform non-parametric segmentation. Histogram backprojection tells us that basing on the color histogram, every pixel location is given a value equal to the histogram value in chromaticity space [1].

We first convert the r and g chromaticity coordinates into integer values and binning the image values in a matrix. The technique of histogram backprojection is shown in snippets of code below.

Lines 1-6 converts the RGB components into chromaticity coordinates. The 2D histogram was made in Lines 8-18. The r and g values were first converted into integers and then binned these image values in a matrix.

The RGB values of the original image was converted to chromaticity coordinates in Lines 22-27. The process of histogram backprojection can be seen in Lines 29-37. In Line 35 the pixel location is given a value equal to its histogram value in chromaticity space. To better understand this concept, let’s discuss the results.

For the CW image, we obtain the following histogram for our patches. The first histogram is for the blue patch and the bottom histogram pertains to the red patch. The NCC image is shown next to the histogram to properly locate the locations of the color of the patches considered.

We can clearly confirm the correctness of the histogram obtained for both patches. These histogram serves as the basis for our new pixel values of the original CW images. Performing histogram backprojection to the CW image, we obtain these results.

The middle image is the result of the non-parametric segmentation of the original image (left most image) for the blue patch. The last image is the result for the red patch. For the blue patch, we can clearly observe the isolation of the blue color of the uniform of Captain America. For the red patch there are some parts that were not segmented. These results proved that the patch used for segmentation matters so much. I feel that if I replace the patch with a better patch, I would obtain much better results.

For the balloon image, I obtained the following histograms for the following patches: blue, green, red and yellow respectively.

We obtain correct histograms for the patches. The results of non-parametric segmentation of the balloon image for each patch is shown below.

Again I believe that improving the patches considered for segmentation, we can have better results. The patches might be uneven or worse, a shade darker or lighter than most of the colors of the images.

Non-parametric segmentation is a more flexible method compared to the parametric method. Because we consider histograms, we could define ROI’s of multiple colors and still effectively segment the image. The parametric segmentation has the limitation of having an ROI of only a single color. Non-parametric segmentation also has a faster processing time since it involves no computation. The 2D histogram contains more reliable information for the pixel values we aim to segment.

After finishing the activity, I felt more skillful in image processing. A new skill such as what we gain in this activity is overwhelming. I just know that somewhere and sometime I would be able to use my new gained skill. I had lots of fun in this activity. I was amazed by my results. I am in awe of how simple the process could be to segment the images with the desired ROI. Soon I’ll add some more results which I would be able to do on some leisure times. I already have ideas on mind and I hope it would bear fruit.

Overall, I give myself 10 points for this activity because I believe I was able to do what is asked. The results I obtained are great and clearly what were asked for. Since I was not able to go beyond what is asked for, I do not deserve some extra points. If anything else, I gained lots of new skills due to these strings of activities we have for AP 186. Thank you Maam for being patient with us through these activities.

PS. I would like to thank Ron Aves, Gio Jubilo and Ralph Aguinaldo for giving me some insights on some parts of the activity.

Reference:

A7 – Image Segmentation, Applied Physics 186 Activity 7 Manual, Dr. Maricor Soriano

Activity 6 – Properties and Applications of the 2D Fourier Transform

In Activity 5, we explored the properties of Fourier transform and the convolution theorem. This time we examine the properties of the 2D Fourier transform and its applications. With more familiarity with the discrete FFT, we expect that we can have some ease with this activity. Though the workload for this activity is much heavier, it provides us with more fun challenges not to undermine the real and awesome image processing skills we expect to obtain from these activities.

Anamorphic Property of FT of different 2D patterns

According to the Merriam-Webster dictionary [2], “Anamorphic” means producing, relating to, or marked by intentional distortion of an image which tells us the kind of results we aim to produce for this part of the activity. Let’s recall that the FT space is in inverse dimension to the original space. We can also recall that what is wide in one axis will be narrow in the spatial frequency axis. This is the anamorphic property of the Fourier transform [2]. Different dimensions along each axis results into anamorphism along each axis independently. We examine the anamorphic property of the Fourier transform.

A tall rectangle aperture is observed as shown in the upper leftmost image. Its shifted FT is shown next to it. As expected a quadrilateral aperture has an FT of a cross like fringe patterns. The bottom image is a zoomed in version of the mat2gray shifted FT of the tall rectangle aperture. The FT shows anamorphism since we can observe the distortion in the image axes. We have a tall rectangle aperture which is wide with respect to the y-axis but we can observe the middle fringe pattern to be wide in the x-axis. To further observe this property of the FT, we observe the wide rectangle aperture.

We can observe anamorphism in the FT of the wide rectangle. The wide rectangle is wide in the x-axis but the middle fringe pattern shows favor in the y-axis. The distortion shows this common property of the Fourier transform.

dot_2

We produce an image of two dots from the center along the x-axis symmetric about the center, both 2 pixels away from the center. This constitutes somehow a double slit for our interference patterns. As expected the FT of this figure are fringe patterns. It is also wide in the y-axis as anamorphism suggests. Changing the spacing between the dots produces such results,

dot_10

The dots are placed 10 pixels away from the center. There are more fringe patterns along the x-axis. The spacing between the dots determines the frequency of the corrugated roof pattern. 5X spacing produced 5X more frequency for the FT fringe patterns.

Rotation Property of the FT

From anamorphism, we observe the rotation property of the Fourier transform. The best way to observe this is through synthetic images of a sinusoid through a corrugate roof pattern. Given the example code in the manual, a synthetic image of a sinusoid in the x-direction was produced. The sinusoid is in the form $sin2\pi f X$ where f is the frequency. Its FT was obtained and the FT modulus was displayed. With a frequency of 4, the sinusoid and its FT is shown below.

unsurprisingly, the FT of the corrugated roof in the x-axis turns out to be two dots arranged in the y-axis. Anamorphism is again shown in this result. When we change the frequency of the corrugated roof pattern, we observe these results.

Fz4

The images of the sinusoid (top) with their corresponding FTs (bottom) are placed in increasing frequency. We can observe that as we increase the frequency of the corrugated roof pattern, the spacing of the two dots to the center along the y-axis is increased. Since digital images don’t have negative values, there is a need to add a bias to our sinusoids to produce real images. Adding some constant bias, the FTs of the corrugated roof in increasing frequencies is shown below.

The pixel in the middle represents the bias I added in the sinusoidals. As we increase the frequency, the spacing between the dots increases as well. So if we take an image of an interferogram for a Young’s double slit experiment, we can find the frequency of the fringe patterns produced by simulating and taking the FT of two dots with the same spacing of the slits in the experiment. From this experiment, we expect to observe a sinusoid and its frequency is the same as the fringe pattern we observe in the actual experiment.

Suppose we add a non-constant bias in the form of a very low-frequency sinusoidal of the form $sin0.4\pi X$ , we obtained the following results. We can observe the spacing of two dots increases as the frequency of the original sinusoid is increased. We can also observe another set of 2 dots in the middle which can be attributed to the very low frequency added. So for an interferogram setup where a non-constant bias is added, we still can determine the frequency of the interferogram by simulation and the use of Fourier transform.

Rotating the original sinusoid by $30^{o}$ , the new sinusoid form is in the form $sin(2\pi f(Y*sin(\theta) + Xcos(\theta))$ . The resulting images and their FTs for different frequencies is shown below.

As observed in previous results, increasing the frequency also increases the spacing between the dots. The FT was also rotated by the same angle as the original image. The rotation property of FT is manifested in these results. The amount of rotation we imply on an image is the same rotation that is implied in its FT.

A combination of two sinusoids of the form $zc = sin(2\pi fX) sin(2\pi fY)$ in different axes and their resulting FTs are shown below.

The spacing between the dots in the FT remain dependent of the frequency of the sinusoid in the axes. We may consider two dots to be one unit and the spacing between the sets of dots are dependent of the frequency of the sinusoid. The results are shown in increasing frequencies in sinusoids in the x-direction with different frequencies in the y-direction.

Combining all the results we gather, I ended up adding several rotated sinusoids to a combination of sinusoids in the previous set of results. The resulting image and its FT is shown below.

zcr

With a combination of two sinusoids and the addition of several rotated sinusoids, we can clearly observe the rotation property of the FT where several rotated FTs and the spacing between the dots occurred in the FT of this abstract image in the left. It is quite amazing how we played with this part of the activity and ended up producing such results. I had so much fun in this part of the activity.

Convolution Theorem Redux

To start this part of the activity, two dots are placed along the x-axis symmetric about the center. From previous results, we know that the FT of this image is a corrugated roof pattern. We add some twist with this activity to further observe the convolution theorem.

Instead of dots, circles were placed symmetric along the x-axis. The FT of the image was taken and observed in different radius of the circles. The results are as follows.

Fcircles2

And voila! In my delight, the results are so good. From the previous blog post, we can recall that the FT of a circular aperture is a Poisson pattern. Placing two circular apertures symmetric about the center much like a double slit setup does not only produce a Poisson pattern but also a fringe pattern enclosed in the Poisson pattern! Such a beauty! We can also observe the difference of increasing radius of circles. Increasing the radius, decreases the size of the Poisson pattern observed.

We replaced the circles with squares of different widths. The FT of a square aperture is a cross like pattern with radial fringes along the x and y axis. I am so excited to see the results of this image and was not disappointed. Here are the results.

Convolution is the real thing. The radial fringe pattern was embedded with another fringe like pattern due to the presence of two square aperture. Also as we increase the width of the squares, the smaller pattern is produced.

Now it gets crazier since we are bound to change the squares with Gaussians of the form $exp(\frac{-(x\pm \mu_{o})^{2}}{\sigma^2})$ of varying $\sigma$ where $\mu$ are the peak locations. The results are as follows.

Fgauss20

The FT of a Gaussian is also a Gaussian. The Gaussian produced still has fringe patterns embedded in it. The larger the $\sigma$ , the larger the size of the FT becomes.

To further observe the convolution theorem, we created an array of 200 x 200 zeroes. 10 random points were filled with 1’s. The 1’s would approximate the dirac deltas. A set of 5, 3×3 patterns were created and was convolved with the array of random 1’s. The results are shown below.

s-rand

s-afft

s-conv

The first two figures shows the array of random 1’s and the spot pattern. Their FTs are directly below their images. The left bottom most image is the convolution of their FTs. We can clearly see the resemblance of the figure with the FTs of the array and patterns. The convolution is the right bottom most image. But since the pattern considered is very small we cannot see the right image. The image supposedly features the pattern placed in the random 1’s. 10 spot patterns should be seen in the locations of the 1’s in the array. But since we can still view the FT of their convolution, we can still conclude that we obtained the right convolution of the array and the pattern. We view other patterns and random arrays.

For a vertical pattern, the results are as follows.

v-rand

For a horizontal pattern, we observe these results.

For a diagonal pattern, these are the results.

A 200 x 200 array of zeroes was made where equally spaced 1’s along the x and y axes are placed. Considering different spacing between the 1’s, the images and their corresponding FT’s are shown below.

A13

A15

A18

As we increase the spacing, we observe more “windows”. These windows are more likely produced by overlapping fringe patterns along both axis. We may also try adding more 1’s in the array and the result of its FT is the presence of more of these “windows”.

Well the main goal of this part of the activity is to show that we can filter an image through its Fourier space domain. Any unwanted repetitive pattern in an image can be filtered by masking their frequencies in the Fourier domain. We can also enhance the image by enhancing the frequencies of desired features. We will further observe this in the next parts of the activities.

Fingerprints: Ridge Enhancement

Supposedly, we are to prepare an image of our own fingerprint for this activity. I was unable to produce one due to lack of a stamping ink and lack of creativity. Honestly, this was my main problem in the activity. I was lazy enough to wait for an image of a fingerprint before I was able to move on with the activity. Luckily, I found my stride to finally search for a fingerprint in the web and found this gem.

Fingerprint retrieved from http://www.creativeclass.com/_v3/creative_class/2008/09/30/get-it-right-puh-leaze/

To properly the ridges of the fingerprint, we obtain the grayscale of the fingerprint. The FT of the grayscaled fingerprint was also observed.

fp-bin

The FT of the fingerprint gives us the idea of the filter we ought to use. We need to retain the two concentric circles in the middle and filter the rest of the FT. Filtering in the Fourier space is one of the most effective way to remove unwanted patterns. In this case, the botches are what we want to remove. The frequencies of the ridges lie on the concentric circles. The filter used is shown below.

The hardest part of making the filter is the estimation of the concentric circles that we ought to retain. When the filter was already made, we convolve the filter and the FT of the grayscaled fingerprint. The resulting convolution is shown below.

We can observe the removal of the botches and the clearer appearance of the ridges. The ridges are necessary since they make anyone’s fingerprint unique. The botches we encountered are unavoidable since there is an uneven distribution of the ink when we capture our fingerprints. Filtering in the Fourier domain provides us an easy way to process and enhance our images.

Lunar Landing Scanned Pictures: Line removal

A 1967 lunar picture is shown below. This picture was obtained by the unmanned Lunar Orbiter V spacecraft prior to the Apollo missions to the Moon. The black and white film was automatically developed onboard the spacecraft and
subsequently digitized for transmission to Earth. The regularly spaced vertical lines are the result of combining individually digitized ‘framelets’ to make a composite photograph and the irregularly-shaped bright and dark spots are due to nonuniform film development [3].

The lines are the unwanted repetitive patterns for this image. We remove this in the Fourier space. The FT of the grayscaled version of the image is shown below.

The lines along the x and y axes are the frequencies of the unwanted repetitive line patterns. We need to retain the small circle in the middle as it contains the important information of the picture. Unlike in the case of the fingerprint, we retain the other areas and just completely eliminate the vertical and horizontal lines in the axes. The filter used for the enhancement of the figure is shown below.

The circle in the middle was effectively filtered and the lines in the axes were eliminated. The resulting FT of the convolution of the filter and the FT of the grayscaled image is as follows.

lun-enhanced

The image on the left side is the product of the filter and the grayscale version of the original image. The right side is the product of the filter applied to the RGB channels of the original image. As we can see for both products, the unwanted repetitive lines are clearly removed using the filter. The method of filtering in the Fourier domain proved to be an effective way of enhancing these images.

Canvas Weave Modeling and Removal

The last part of the activity directs us to modeling a canvas weave and eventually enhancing a painting by removing the said unwanted part of the image. The image considered is shown below.

As we can observe, the image of the painting has the obvious patterns of the canvas weave. The pattern is what we aim to remove to enhance the detail of the oil painting. The FT of the grayscale version of this image is given below.

The unwanted repetitive pattern given by the canvas weave is defined by the blots in surrounding the middle area of the FT. These are the patterns we need to remove from the FT image while retaining the entire area, the lines in the axes and the circle in the middle. Using GIMP, I covered these blots using black squares. The filter produced in the process is shown below.

Applying the filter to the FT of the grayscale image of the oil painting, we obtained the FT of the convolution given by the images below.

weave-enhanced

The left side is the product of the filter and the grayscale image of the oil painting. The right image results from the application of the filter to the RGB channels of the original image. For both results, we observe that we have completely removed the canvas weave pattern. The brushstrokes are also improved as observed in the colored result. We completely enhanced the image using the method of filtering in the Fourier domain. If we inverse the filter and convolve it with the FT of the image of the oil painting, we would get the canvas weave pattern. We can therefore conclude that inversing the filter, we could obtain the unwanted repetitive patterns we removed from the images.

weave-invfilter

The activity was a whole lot of fun. I want to thank Ralph Aguinaldo, Ron Aves, Gio Jubilo, Martin Bartolome and Jaime Olivares for helping me realize some mistakes I made in my Scilab codes. They also provide suggestions most especially on the last 3 sets of activities of enhancing images by filtering in the Fourier domain. Honestly, I overthinked a lot of these activities. The activity made me realize that some things even how complicated it may seem, is just simple as saying 1-2-3. I feel like I would have completed the activity much earlier if I did not give too much time in finding ways to produce an image of my fingerprint.

Overall, the activity was both stressful yet fulfilling. Since I completed every part of the activity and produce very good results, I would give myself a 10 for this activity. I believe, I was also able to place good insights about the theories behind the results obtained for this activity. I also know that I do not deserve extra points due to the punctuality of my blog. But still, regardless of points, I feel really cool producing my results. And nobody would stop me from feeling this way.

References:

A6 – Properties and Applications of the 2D Fourier Transform, Dr. Maricor Soriano, Applied Physics 186 Manual
Anamorphic, http://www.merriam-webster.com/dictionary/anamorphic
Lunar Picture from Lunar Orbiter V spacecraft, http://www.lpi.usra.edu/lunar/missions/apollo/apollo_11/images/

Activity 5 – Fourier Transform Model of Image Formation

The activity gave us the opportunity to explore more on different properties of the Fourier transform and the convolution theorem. This time we are not restricted to integrals and a bunch of functions but we were given the chance to oversee the simulations itself. These simulations included the use of synthetic images which were manipulated for our purpose. It was a very fun and challenging activity since we are able to understand these concepts using different simulations of synthetic images. We can only confirm our results by understanding the nature of these concepts. Since the synthetic shapes are common, there are known analytical Fourier transform (FT) of these shapes which can be used to confirm the obtained results.

Familiarization with discrete FFT

The first part of the activity involves getting cozy with the discrete Fourier transform (DFT). Good thing, because the software we used, Scilab has a built-in function for the Fast Fourier transform (FFT), fft2, which takes care of our discrete Fourier transform. From the word discrete, I already assumed it involves discrete parts of the original image used to convert the original domain to the frequency domain. We took the FFT of some synthetic images and investigate on the new images we produced.

The first synthetic images we ought to manipulate are the Scilab-produced circle of certain radius and a Paint-produced image of the capital letter “A“. To start things off, we produced the synthetic image of the circle using the technique we used in previous activities. The image for “A” was produced in Paint by setting its properties to 128 pixels x 128 pixels and placing a white letter “A” in the middle of a black background. The synthetic images for this activity are all in 128 x 128 bitmap format. We took the FT of these figures and displayed their intensity values using the absolute value function, abs(). Since the output of FT has quadrants along the diagonals interchanged, we need to apply fftshift() to our resulting intensity values to rearrange the quadrants back to normal. The results are as follows.

Note: For this entire part of the activity and for each synthetic image, the leftmost image pertains to the original Scilab or Paint produced image. The next image is the FT of the synthetic image while the next image is the grayscale shifted version of the FT. The last image refers to the application of FT twice to the synthetic image. Also more often I would deal with the shifted FT of these images since these images are of interest for this activity.

circle_2fft circle_fft circle_shift

A_fft A_shift

We can observe that the FT of these images definitely shows the interchanging of the quadrants along the diagonals. Upon shifting the obtained FT and converting the values to grayscale, we certainly can observe the real FT of these images. As for the FT of the circle, we can observe a known phenomena called Poisson spot as the pattern being shown. Poisson spot happens when a light is blocked by any circular aperture. This is consistent with the analytical FT of a circle. From this point, I can infer that if we consider our shapes as aperture, the FT of these shapes produced the interference pattern if a light strikes these apertures. Upon trying different radii for the circular image, I observed an interesting pattern in the results. The larger the radii, the smaller the observed spot is. This is true for interferometry where the smaller the aperture, the more visible the interference pattern that could be produced.

I cannot simply tell the same for the image of A since we never have an aperture of such shape but we can also use our intuition that based on its FT, we may have a case here about FT producing the interference patterns if the shapes are considered as apertures. The last images shows that the inverse FT is the same as the forward FT with the image inverted. This property can clearly be observe with the image of A.

To show that the FT of any function is complex, it is necessary for us to show the real and imaginary parts of the FT of the circle and image of A. The first 2 images are for the circle and the last 2 is for the image of A. The leftmost images for each are the real parts of the FT while the next images are the imaginary parts of the FT. From these images we can clearly confirm that the FT of any function is complex.

circle_real circle_imag

The next shape we simulated is the sinusoid along x more like a corrugated roof. The results are as follows.

sin sin_shift sin_2fft

The most tricky image for this activity is this sinusoid. I believe a lot of people in class including me experienced a hard time obtaining an acceptable result for the FT of this image. We never considered the fact that the periodicity of this function ranges from -1 to 1. A bias was needed to lift the negative values of the function. Normalization was also necessary to dictate the range of the values as 0 to 1. I personally want to thank Dr. Soriano and Mario Onglao for shedding some needed light in this particular shape of interest. If we look closely at the FT of the sinusoid, we can find it at the top of the image. Shifting the obtained value, we can observe 3 dots. The analytical FT of a sine function with the form $sin2\pi kx$ includes the Dirac delta function with peaks at k and -k. The obtained FT clearly shows the equally spaced dots from the center pertaining to the frequency of the sinusoid, k. The last image also follows the relationship between the inverse and forward FFT.

The next shape considered is the double slit. The process of doing the synthetic image in Scilab was fun because I thought of ways to make the slit as thin as possible yet I believe I made a blunder by putting too much distance between the slits.

slit slit_shift slit_2fft

Again, the FFT lies on top of the entire black background. The third image shows the shifted FT of the double slit. We can observe a fringe pattern very common to the double slit. The fringe patterns are produced when a light strikes the double slit which causes interference among the waves. The hypothesis I created a while ago now more strongly suggests that the FT of these shapes produces patterns that in real situations happens when we consider a light striking the aperture with the shape of the considered figure. We can also observe that it seems like a Gaussian wave guides the pattern. Much like a beat, a larger sinusoid covers the fringe patterns as we can observe the difference in intensity between the patterns in the middle with those in the outer area of the shifted FT. I also want to thank Mario Onglao for pointing this concept to me while we were discussing the right result for this shape.

The next shape I would discuss is the square shape. The results are as follows.

square

If we were able to zoom in at the FT of the square shape, we might be able to see a cross shape pattern with the middle part of the pattern with the highest intensity. The change of intensity varies radially along the x and y axes. The same can be observed when we consider a cross shape aperture.

The last image considered for this part of the activity is for the 2D Gaussian bell curve. The results obtained are as follows.

gauss

Before I discuss the results for this synthetic shape, I would like to thank Dr. Soriano for pointing out my mistakes in the code for this simulation. I forgot to include a σ in the Gaussian equation. Also the mesh in Scilab was helpful for checking the correctness of the Gaussian bell produced. The FT of this shape is also a Gaussian curve of larger area. When we apply the FT inversely, we also obtained a Gaussian function of larger area. This is consistent with the analytical FT of the 2D Gaussian bell where we really obtain another Gaussian with a larger area.

Simulation of an imaging device

This part of the activity projects the properties of the concept of convolution. In particular, the linear operation can be represented in linear transformations such as Laplace or Fourier. We can observe convolution by simply multiplying the FTs of the functions of interest.

Using Paint, a 128×128 bitmap image of the word “VIP” was created. A circular image of a certain radius was also made using Scilab. We load these images in Scilab and obtained their FTs. Since the circle is already in the Fourier plane, we only obtained the shifted FT of the circle. The circle serves as the aperture of the circular lens. I believe this is the part where I would be able to confirm my hypothesis a while ago that FT serves as a lens for the patterns created for an aperture of certain shapes.

We get the product of their FTs and to observe their convolution we get the inverse FT of the product. We tried this for different radii of the circle. These are the results by using circular apertures of radius 0.3 to 0.9 with intervals of 0.1. The order of results is increasing radius from left to right, top to bottom.

VIP

FFT6

The first image is the original “VIP” image produced in Paint. As we can observe with the results, with increasing radius of the circle, the clearer the image. As expected, this should be the result since increasing the size of the aperture should allow a higher of intensity of light to pass through. The image also has the properties of both the circle and the VIP image. The results are also consistent with the relationship between the inverse and forward FFT.

Template Matching using Correlation

Correlation is similar to convolution by having a correlation theorem which also holds for linear transformations. It has basically the same form as the convolution but a term is conjugated. The process is the same and the change we make is to obtain the complex conjugate of the FT of the image of interest. The image of interest is shown as the first image below.

msg

The image of A has the same font and font size as the phrase shown in the image of interest. Correlation measures the degree of similarity between two functions. The more identical the functions at certain coordinates, the higher their correlation value at that coordinate is. The concept of correlation is mostly used in template matching or pattern recognition. The aim of this part of the activity is to numerically obtain the correlation of these two images. The result of their correlation is shown below.

We can observe that the parts of the image with the highest intensity are those areas where a letter “A” is located. Definitely the correlation of the images are obtained using the given process. We can definitely use Fourier transform and the correlation theorem for template matching and pattern recognition given that we have the image of the desired pattern or template.

Edge detection using the Convolution Integral

The last part of the activity aims to combine the concept of convolution and the correlation theorem to perform edge detection. We use the concept of template matching in correlation to find edge patterns in an image. The image of interest is the VIP image used for the 2nd part of the activity.

A 3×3 matrix pattern of an edge is made using Scilab. The values inside the matrix has a total sum of zero. This pattern was placed in the middle of a 128×128 black background image. Different patterns were produced: horizontal, vertical, diagonal and a spot pattern. The images containing the patterns are convolved to the VIP image. The results are as follows:

1horizontal

The first image is produced by the image containing the horizontal pattern. We can observe that correlation is achieved since we can see the emphasis or the higher intensity of values in the horizontal areas of the VIP image. The highlight of the image lies on the horizontal areas. We can also observe this in the 2nd image, produced by the vertical pattern containing image. The 3rd resulting image produced by the diagonal pattern containing image also highlights the diagonal areas of the VIP image. The spot pattern image produced the 4th image giving us the edge of the VIP image. I found it cool that the spot pattern gave us the entire edge of the VIP image. It means that we can get the edge of any image by convolving it with an black image with a spot pattern centered in it.

The activity provided a lot of fun and anxiety as well. I thought some of my results are blotched or mistakes but I found some relief by asking some of my classmates. I want to thank Ron Aves for providing me with some tricks for Scilab to read the right kind of data type for my images. Hats off to Ralph Aguinaldo who confirmed my results in the template matching part. All along I thought I made a mistake but then I realize that the intensities should really be high at different parts of “A” in the image. Also I made a mistake of not placing the 3×3 patterns in the middle of a 128×128 black image which made me wonder why my code won’t work. And of course I want to thank Dr. Soriano for providing inspiring messages and short motivational speeches to boost our morale.

Overall, I give myself a 10 for the effort I gave for this activity. I think I allotted enough time to accomplish this activity. I don’t deserve extra points since I stuck to the required tasks and did not try anything beyond the required tasks. But overall I am happy with the new lessons and techniques I learned through these activities.

Activity 4 – Length and area estimation in images

The objective of this activity is to use various softwares to measure area and length of images. To apply the skill acquired, we measured the area of a chosen building or any place of interest. I captured an image of the place using Google maps and measured its area using a scale for pixel to unit length ratio. We used Green’s theorem to measure the area of any image by using edges of the shape of interest. Morphological operations are the second technique used for this activity. These operations consider connected pixels as blobs. The area is calculated by counting pixels in the blob. The software used to measure length and area of images are Scilab 5.5.1 and ImageJ.

Green’s theorem is mathematically given by the equation:

$A=\frac{1}{2}\sum\limits_{i=1}^{N_b} [x_{i}y_{i+1}-y_{i}x_{i+1}]$

The equation tells us that the area can be computed by finding the coordinates of the edge of the shape by slicing the shape into “pie slices”. The adjacent edge coordinates are considered for each element of the summation. The sum of these elements gives us the area of the shape.

We verified the theorem by producing synthetic images in Scilab. The area of these images are analytically known. I produced 3 shapes: a circle, a square box and an ellipse. A Scilab code was produced based on the Green’s theorem to calculate the area of these shapes. I would like to recognize the help given to me by Ron Aves and Jesli Santiago in producing this Scilab code. I had a hard time thinking of how to sort the polar angle of the edges of the shapes with its respective x and y coordinates. Thank you for giving me a tip on how to collapse these matrices into a single matrix consisting of these important values.

After producing the figure, the image is loaded in Scilab. We find the edge using the command edge in Scilab. The method that proves to be most effective in our figures is “canny”. We record the pixel coordinates of the edge of the figure. Using these coordinates we take the polar angles of the coordinates then sort the coordinates with their respective polar angles to place adjacent coordinates next to each other. For these synthetic figures, I did not use the concept of the centroid since these figures are already centered.

Upon sorting the coordinates, Green’s theorem was used to compute for the area in pixel units. The data gathered for each figure is as follows:

Circle -> radius = 0.7 -> Real Area: 1.5393 -> Scilab Area: 1.5387 -> Deviation: 0.04%
Square -> length = 1 -> Real Area: 1 -> Scilab Area: 1.001 -> Deviation: 0.1%
Ellipse -> a = 0.707, b = 0.767 -> Real Area: 1.7038 -> Scilab Area: 1.7031 -> Deviation: 0.04%

The deviations are very small that is why we can verify that Green’s theorem using edge coordinates of the shapes. After doing this I felt so happy just like this kid.

The next activity aims to use ImageJ to measure area. I was a bit surprised on how light the program is. It is also very user-friendly. The objective is to measure the area of a scanned image knowing the analytical area of the scanned object. I used my UP ID for this part of the activity. I would like to apologize for anyone who would be viewing my ID. I hope you’re ready in what you are about to see. Haha.

My ID has dimensions of 86 cm x 54 cm. Its area is 4644 $cm^{2}$ or 0.4644 $m^{2}$ . Knowing the length of the ID, I drew a straight line to the length of the image. I set the scale by using Analyze > Set Scale… placing the known distance. The scale is given by 1169.14 pixels/m. By placing a polygon (rectangle) in the ID, we measured the area by using Analyze > Measure. The computed area for the ID is 0.455 $m^{2}$ with a deviation of 2.02%. We can observe that ImageJ computed a well accurate area of the scanned object.

To wrap up the activity, we aim to compute the area of a desired building or location. I chose the National Theater or the Tanghalang Pambansa in the CCP Complex. The building’s image in Google Map is shown below.

I cropped the scale for me to check the area of the building in ImageJ. This scale is used to supply a known distance in the ImageJ program. The Scilab code used to measure area by Green’s theorem was also used to measure the building’s area. I faced a dilemma since I could not find the area of the National Theater. I never found the exact area of the building.

So to check the area of the building, I assumed that the exact area of the building is the computed area using ImageJ. Since I proved that accuracy is not a problem in the ImageJ mechanism of computing the area, I believe I can use this area. The scale used by ImageJ was 3.45 pixels/m. I loaded the figure in Scilab and modified the code by considering the centroid of the figure. I was not sure if the bitmap figure of the building is centered.

The Scilab code used for this part of the activity is shown above. The bitmap image was created using GIMP. I would like to thank Jaime Olivares for helping me in editing the image to convert it into bitmap. Also credit is due to Robert Tacbad for helping me in completing my code adpating the concept of the centroid.

By running the Scilab code, I obtained an area of 97692.167 $pix^2$ . Using the scale in ImageJ, I converted the pixel area in to real area. The computed Scilab area is 8207.7015 sq. meters. Using ImageJ, I was able to compute an area of 8191.388 sq. meters. I obtained a deviation of 0.2%. I could say that the Scilab code was effective in computing the area of the National Theater of the Philippines.

For my self-evaluation, I give myself a 9 of 10 since I finished the activity with good results. The 1 point I deducted is due to the punctuality of my work. I should have finished this activity last Friday or at least this weekend. I hope I can cope up in the next activity. I enjoyed doing the activity except for the image editing which took me so long. I really have no skills on image editing. Converting the image from Google Map into a bitmap image took me a lot of hours. It was a real challenge and I am really glad I was able to make it. Thank you Maam for this activity. 🙂

Activity 2 – Digital Scanning

Our goal for this activity is to reconstruct a hand-drawn graph to a digital graph using the concept of ratio and proportion in pixel and physical values. From pixel values we must acquire a relationship that would relate the pixel values to the actual physical variables in the graph.

The truth is the hardest work I encountered in this activity is finding a hand-drawn graph. We tried going to NIP library to find a hand-written graph. We found some old thesis and journals but we were not satisfied with the graphs we saw. We thought that we need a really obvious hand written graph. Actually, the process of finding the graph was really frustrating. We approach the last day of the week and we haven’t found any graph yet. Good thing is that Robert Tacbad and Jaime Olivares were with me when I visited the CS library to find some really old thesis. It was full of very old journals and published works. We came through a shelf that were published from 1950-1960. Jackpot! Then we came through another problem, the sensitivity of rules about these works restricted us from simply photocopying or scanning the graphs we found. We thank the CS staff members that were very understanding. You da real MVPs. At last they understood that we would not in any way plagiarize or use these graphs for any to-be-published work. We promised we will cite our references. The graph I obtained came from a thesis by a graduate student named Nieves Portugal-Dayrit entitled “The Microbiological Assay of Amino Acids in some Philippine Legumes” published in February 15 1956. My grandpa was just 12 years old back then. Wow!

The process of reconstructing the graph started by producing a digital image of the graph. We had a photocopy of the graph from CS and finally we scanned it in our laboratory to acquire our image. I cut the obtained image to focus on the graph itself. Using GIMP 2.8, I acquired pixel locations of the x and y axes of the graph. I must say that I am very lucky since the film used to plot the graph has some grids that made it easy for me to acquire pixel locations. Using these data, I acquired an equation that relates the physical variables to the pixel locations. For the x axis variables, I obtained an equation: x_phy = 0.0062x_pix – 1.2081 while for the y axis variables: y_phy = 0.0025y_pix – 0.4993 where subscripts phy pertains to physical variables and pix to pixel variables.

I turned my attention to the graph itself. I acquired the pixel locations first of notable locations of the graph. I tried to graph the obtained data and observed that the first graph was still rough. I collected more pixel locations in the graph summing up 22 points in the graph. I plotted the obtained data and observed that the graph somehow resembles the original graph. The first graph I obtained has axes in pixels.

Using the equations for the relationship of the physical variables and pixel locations, I converted the axes into physical variables. The next step is to confirm the similarities of the original and the digitally reconstructed graph. Using Microsoft Excel, I overlaid the image of the original hand written graph to my digital graph. By placing offsets to align the axes of the image and the graph, I confirmed that I obtained the same graph as the original hand-written graph. From this confirmation, I give myself a 10 for this activity. I also want to note that the axes of the original image have the same axes values with the Excel graph. The values were obtained from the equation.

Reference:
N. Portugal-Dayrit, “The microbiological assay of amino acids in some Philippine legumes,” College of Science, University of the Philippines Diliman, 1956.

Activity 3: Scilab Basics

Activity 3 tackles with us playing with Scilab. Honestly, I have little knowledge of the software since I used this software for an activity last semester for our Applied Physics 185 class also with Dr. Soriano. But what I did last year was different since it involves Fourier transform and the synthesis of sounds. What we aim for this activity is to create synthetic images with the use of matrices and basic arithmetic. We were given an example of a Scilab code to create a circular aperture or a pinhole. The image produced shows a black background and the white circular portion pertains to the aperture. Basically, we aim to produce different images with this style.

The task given to us was to produce 7 specific images. It was a fun activity since it relies on our imagination and wit on how to construct these images. At first I don’t have an idea of how to construct these images since I still worry about the basics of programming in Scilab. But I was grateful for the example given by Dr. Soriano because it made sense on how to construct these figures. And I want to thank all my classmates since we brainstormed our way into the light, that is, the basic things we need to know in producing a program to construct these figures.

The first figure I was able to construct is the ellipse. It was the easiest to figure out since we are already given the code for our circular aperture. I just reduce one variable to a fraction for our circular aperture to be an ellipse. It follows the equation for an ellipse knowing that a circle is a special case of the ellipse. I tried to produce a diagonal ellipse but I failed to do so since my code does not work due to an issue of the use of the element-by-element operator “.” when doing the operations. The centered square aperture and the cross were somewhat connected. I constructed the cross figure by thinking of strips. I imagined two strips in the center parallel to x and y axes overlapping to form a cross. I also tried to make a smaller version of this cross and came up with a new figure. This figure symbolizes more of the cross we commonly know. With this idea, I immediately thought of how to construct the square. I first built a strip parallel to the x-axis then cut the strip in its end to construct the square. I made sure that sides of the square are equal.

Using the example of the circle, I thought of just placing a black smaller circular aperture in the constructed circle. This formed the annulus and voila I completed another figure. At this point, I am starting to enjoy the process of learning the basics of Scilab since I am getting the feel of it. I stopped a bit when I tried to figure out how to construct the sinusoid along the x-direction. The corrugated roof seems a little complicated for me. I would like to thank Martin Bartolome and Jesli Santiago for giving us some tips for the 2 of the last 3 figures. Since it was obvious that we need a sinusoid for the corrugated roof, we just simply plotted a sinusoid knowing that it is periodic in nature. I was surprised that it was that simple. I was happy and worried at the same time since I think I am overthinking the process of constructing these figures. From the sinusoid, we can easily build the grating along the x-direction. By adding a grid of zeroes, for every certain value (0.8 for my figure) of the sinusoid, we replace the value of that sinusoid coordinate in our zero grid by 1. From this we produced the grating along the x-direction.

And at last I am about to construct the last required figure. Then it hit me, it is not simple. How do I make a circular aperture with graded Gaussian transparency? Jaime and I tried to find sources of how to do this. We searched the internet and tried the steps shown in our sources but to no avail. Upon searching for a Gaussian entry in the help window of Scilab we encountered the equation that describes the Gaussian distribution. I thank Jaime for pointing out that we can use the equation of the Gaussian transparency to form a “ripple-like” figure then we replace the values to 0 while retaining a circular aperture in the middle by applying the concept of the example given to us. In short, we first constructed a ripple effect in the grid then cover everything except for a circular aperture in the middle. I’m done! It was fulfilling to construct all these figures. Thank you maam for bringing fun to learning. It was refreshing in some way with all the stress of the past semesters at least I can say that I had more fun in this one.

I tried to play with our codes and I constructed different figures. From my code for the square aperture, I constructed a star like figure. I also tried to construct some strips. I tried some other figures but I failed to do so. I believe I deserve a 10 for this activity because I successfully constructed all the required figures. I think I also deserved an extra point since I tried to play with the figures. I had fun with this activity so I believe I deserve these self-given points.